GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE

GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE

L’histoire des courbes planes est intimement liée à l’histoire et aux développements du calcul infinitésimal, et les premiers résultats obtenus au XVII^e siècle sont directement issus de considérations géométriques et cinématiques (cf. CALCUL INFINITÉSIMAL – Histoire). Les courbes dans l’espace à trois dimensions (dites à «double courbure») ont été étudiées par Clairaut (1731). C’est Monge qui, dans un mémoire présenté en 1771, introduisit les notions fondamentales de rayon de courbure et de surface réglée développable engendrée par les tangentes à une courbe gauche. En 1826, Cauchy définit la normale principale et donna des expressions de la courbure et de la torsion. Enfin, Frénet (1847) et Serret (1850) démontrèrent l’équivalent des formules qui portent leur nom.

Les surfaces, pour leur part, ont été au XVIII^e siècle une occasion naturelle de développer les fonctions de plusieurs variables. Euler, Monge admettent implicitement l’existence du plan tangent, qui est établie par Dupin en 1813 et reprise par Cauchy (1826). L’étude de la courbure entreprise par Euler (1760), qui introduisit les directions principales, a été approfondie par Meusnier (1776), Monge (1784) qui introduisit les lignes de courbure et Dupin (1813) qui introduisit les directions conjuguées et l’indicatrice qui porte son nom.

La contribution fondamentale de Gauss (Disquisitiones circa superficies curvas , 1827) donna un nouveau visage à la géométrie différentielle. Il utilisa une représentation paramétrique des surfaces (amorce de la notion de carte locale) et dégagea le caractère intrinsèque de la courbure totale; tous les résultats du chapitre 6 lui sont dus. Enfin, le tournant décisif est dû à Riemann (Sur les hypothèses qui servent de fondement à la géométrie , 1854) qui surmonta les difficultés rencontrées pour donner une définition globale mathématiquement satisfaisante des courbes et des surfaces en introduisant la notion de variété à n dimensions ^{[cf. VARIÉTÉS DIFFÉRENTIABLES]}.

On se bornera dans cet article à l’étude des courbes et surfaces plongées dans l’espace euclidien à deux ou trois dimensions. Les définitions correctes exigent l’emploi du théorème des fonctions implicites, c’est pourquoi on introduira d’abord ici la notion d’arc paramétré, dont l’image est une trajectoire, puis on effectuera l’étude locale; la notion de courbe s’obtiendra ensuite en «recollant» de manière régulière une réunion de trajectoires. On définira de même les surfaces en recollant entre elles des images de représentations paramétriques régulières; on introduira les deux formes fondamentales (l’ensemble de ces deux formes définit localement la surface à un déplacement euclidien près) et la courbure totale (qui ne dépend que de la première forme fondamentale). Cette courbure totale joue un grand rôle, tant dans l’étude locale (position par rapport au plan tangent) que globale (caractéristique d’Euler-Poincaré) des surfaces.

1. Sur quelques propriétés de l’espace euclidien

La structure E³, d’espace euclidien de R³ est définie par le choix du produit scalaire usuel pour lequel la base canonique 﨎¹ = (1, 0, 0), 﨎² = (0, 1, 0), 﨎³ = (0, 0, 1) est orthonormée (cf. GROUPES – Groupes classiques et géométrie); la norme de X = (x, y, z ) est alors:

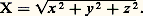Un déplacement euclidien D est une application affine de R³ dans R³ telle que l’application linéaire associée soit une rotation , c’est-à-dire une transformation orthogonale de déterminant égal à 1; l’ensemble des déplacements euclidiens forme alors un groupe , produit semi-direct du groupe additif R³ (groupe des translations) et du groupe O⁺(3, R) des rotations. Un déplacement euclidien est défini par les trois composantes (a ¹, a ², a ³) de la translation et les éléments a ^{j i} d’une matrice orthogonale de déterminant 1. On appelle mouvement euclidien une application t 料 D^t d’un intervalle I de R dans le groupe ; ce mouvement sera dit différentiable de classe C^k si les fonctions t 料 a ⁱ (t ) et t 料 a ^{j i} (t ) définissant ce mouvement sont des fonctions k fois continûment dérivables de t . Dans une interprétation cinématique, le paramètre t désigne le temps. Dans ce qui suit, nous adopterons le langage de la cinématique (vitesse, accélération) pour un paramétrage quelconque.

Un repère 淪 (M, e ¹, e ², e ³) de l’espace euclidien E³ est le transformé par un déplacement D du repère canonique (O, 﨎¹, 﨎², 﨎³); (e ¹, e ², e ³) est donc une base orthonormée de E³ (considéré comme espace vectoriel) de même sens que ( 﨎¹, 﨎², 﨎³), ce qui oriente l’espace. De plus, étant donné deux repères 淪 et 淪 , il existe un déplacement euclidien et un seul transformant 淪 en 淪 .

À un mouvement euclidien t 料 D^t correspond un repère mobile 淪^t = D^t ( 淪⁰) (on peut également définir un repère dépendant de plusieurs paramètres) défini par:

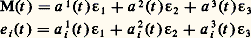pour i = 1, 2, 3; si on rapporte les vecteurs dérivés d M/dt et de ⁱ /dt au repère mobile, on a, en utilisant le fait que d (e ⁱ . e ^j )/dt = 0:

Le vecteur 諸 de composantes (p, q, r ) est le vecteur rotation instantanée du mouvement ^{[cf. CINÉMATIQUE]}; pour tout vecteur V lié à 淪^t, c’est-à-dire tel que:

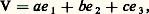où a, b, c sont des constantes, on a alors:

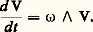On démontre que toute application continue d’une partie de E³ dans E³, qui est une isométrie (c’est-à-dire conserve la norme), est une restriction de déplacement euclidien ou d’antidéplacement (transformation affine dont la transformation linéaire associée est orthogonale de déterminant 漣 1).

Rappelons enfin (cf. CALCUL INFINITÉSIMAL – Calcul à plusieurs variables) qu’une application f d’un ouvert U de R^p dans R³ est dite différentiable de classe C^k si f s’exprime au moyen de trois fonctions numériques, f = (f ¹, f ², f ³), admettant des dérivées partielles continues jusqu’à l’ordre k . La différentielle Df (a ) de f au point a = (a ¹, a ², ..., a ^p ) 捻 U est l’application linéaire de R^p dans R³ définie par:

pour h = (h ¹, ..., h ^p ) 捻 R^p ; on considérera souvent la forme quadratique associée à la différentielle seconde en a , définie par:

on appelle application affine tangente en a à f l’application affine T^a f définie par:

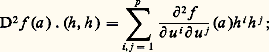
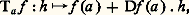ce qui équivaut à: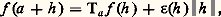

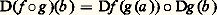où 﨎(h ) tend vers 0 quand h tend vers 0.

Rappelons enfin que, si on compose deux applications différentielles g et f , on a:

et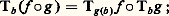

en particulier, si Dg (b ) (et par suite T^b g ) est une bijection, alors T^b (f 獵 g ) et T^g(b) f ont la même image. Dans le cas particulier où g est une fonction d’une variable, alors on a:

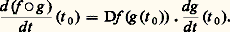2. Remarques sur les courbes et les surfaces

On a une notion intuitive de «courbe» dans l’espace euclidien à 2 ou 3 dimensions: une courbe de E² est définie par une équation F(x , y ) = 0, ou y = f (x ); une courbe de E³, est définie par deux équations z = g (x ) et y = f (x ), ou F(x , y , z ) = 0 et G(x , y , z ) = 0. De même, une «surface» de E³ est définie par une équation z = f (x , y ), ou F (x , y , z ) = 0.

Mais, si on veut préciser ces notions, des difficultés surgissent. Par exemple, le cercle de centre O et de rayon R est l’ensemble des points de E² dont les coordonnées vérifient l’équation:

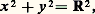mais on peut aussi représenter ce cercle par:

or l’application ainsi définie de l’intervalle fermé [0, 2 神] sur le cercle n’est pas biunivoque, car les extrémités de cet intervalle sont appliquées sur le même point A (1, 0) du cercle. Or, ce point ne présente aucune singularité sur le cercle.

De même, la sphère de centre O et de rayon R est l’ensemble des points de E³ dont les coordonnées vérifient:

mais elle peut aussi être représentée par: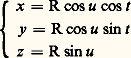

pour 0 諒 t 諒 2 神 et 漣 神/2 諒 u 諒 神/2, les courbes u = constante étant les parallèles et les courbes t = constante étant les méridiens. Mais l’application ainsi définie d’un rectangle de E² sur la sphère n’est pas biunivoque: les «pôles» P (0, 0, 1) et P (0, 0, 漣 1) correspondent respectivement à u = 神/2 et u = 漣 神/2, t quelconque; pourtant les points P et P ne présentent aucune singularité sur la sphère.

Par contre, le cône de révolution d’axe Oz d’équation:

est en correspondance bijective avec le plan d’équation z = 0, cette correspondance associant au point m (x , y ) le point M(x , y , z ) tel que: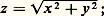

pourtant ce cône présente un point singulier qui est son sommet.

3. Arcs paramétrés et trajectoires

Nous allons distinguer à présent les notions d’arc paramétré et de courbe régulière.

On appellera arc paramétré de classe C^k une application f d’un intervalle I = [a , b ] de R dans E² ou E³ qui soit k fois continûment dérivable dans I (en a et b , on considère respectivement les dérivées à droite et à gauche); dans ce qui suit, on supposera k assez grand pour que toutes les dérivations effectuées aient un sens. On appelle trajectoire de l’arc paramétré f le sous-ensemble image A = f (I).

On dira que deux arcs paramétrés (f , I) et (g , J) de classe C^k sont C^k -équivalents s’il existe un C^k -difféomorphisme 﨏 de I sur J (c’est-à-dire une bijection k fois continûment dérivable ainsi que son inverse) tel que:

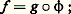cela entraîne en particulier que les deux arcs ont la même trajectoire. On dira que le changement de loi de «temps» 精 = 﨏(t ) est un changement de paramètre admissible . Pour tout t 捻 I, on a d 﨏/dt 0; les paramètres admissibles se répartissent donc en deux classes: ceux pour lesquels d 﨏/dt 礪 0 et ceux pour lesquels d 﨏/dt 麗 0. Choisir un signe revient à orienter la trajectoire.

Exemples

Considérons le «trèfle à quatre feuilles»:

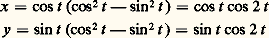pour 0 諒 t 諒 2 神; l’origine O est un point multiple pour la trajectoire, car on a x = y = 0 pour t = 神/4, 3 神/4, 5 神/4, 7 神/4 (fig. 1).

Soit maintenant, pour t 捻 R, l’arc paramétré:

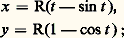la trajectoire est composée d’arcs se déduisant les uns des autres par translation. C’est la cycloïde , trajectoire d’un point lié à un cercle qui roule sans glisser sur une droite (fig. 2).

Points réguliers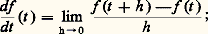

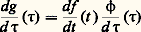Soit f : IE³ un arc paramétré. On appelle vitesse à l’instant t le vecteur dérivé:

si on change la loi de temps, t = 﨏( 精) et g ( 精) = f ( 﨏( 精)), on a:

et les vecteurs (df /dt )(t ) et (dg /d 精)( 精), par suite, sont colinéaires ou simultanément tous deux nuls.

Si (df /dt )(t ) n’est pas nul et si t est un point intérieur à I, la droite portant le vecteur vitesse s’appelle la tangente en M à la trajectoire. Si I = [a , b ], on dit que l’arc est fermé lorsque f (a ) = f (b ); remarquons que, même si en tout point la dérivée est non nulle, la trajectoire peut ne pas avoir de tangente en f (a ) (par exemple si x = cos t cos 2 t , y = sin t cos 2 t pour 神/4 諒 t 諒 3 神/4).

Si t est intérieur à l’intervalle I et si f (t ) 0, on dit que le point f (t ) est un point régulier de la trajectoire; cette propriété se conserve par changement de paramètre admissible. Il résulte alors du théorème des fonctions implicites (cf. CALCUL INFINITÉSIMAL – Calcul à plusieurs variables) qu’il existe un intervalle I¹ 說 I contenant t tel que la restriction de f à I¹, soit injective: par exemple, tous les points du cercle x = R cos t , y = R sin t sont des points réguliers et la restriction de f à

est injective pour tout t .

Pour un arc paramétré, le vecteur d ²f /dt ² représente l’accélération. Dans un changement de paramètre admissible, on a, pour g ( 精) = f (t ):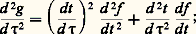

ainsi, si les vecteurs df /dt et d ²f /dt ² ne sont pas colinéaires, le vecteur d ²g /d 精² appartient au plan engendré par ces vecteurs, appelé plan osculateur à la trajectoire au point f (t ).

En un point régulier, désignons par p le plus petit entier 閭 2 tel que le vecteur d ^p f /dt ^p soit non nul et non colinéaire au vecteur vitesse df /dt ; au voisinage d’un tel point, la trajectoire présente l’aspect indiqué sur la figure 3: le point est dit ordinaire si p est pair; si p est impair, la trajectoire «traverse» la tangente au voisinage du point et on dit qu’il y a inflexion . Le cas où df /dt et d ²f /dt ² sont colinéaires se ramène au précédent, car on peut trouver, dans un intervalle I¹ 說 I contenant t , un changement de paramètre admissible tel que d ²g /d 精² soit nul.

Points singuliers

Soit maintenant t ⁰ une valeur du paramètre pour laquelle le vecteur vitesse est nul; on dit que le point f (t ⁰) est un point singulier . Soit p et q, p 麗 q , les plus petits entiers tels que les vecteurs:

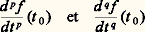soient tous deux non nuls et non colinéaires.

Pour p impair , posons 精 = (t 漣 t ⁰)^p ; on définit ainsi un changement de paramètre qui est un homéomorphisme, mais qui n’est pas admissible au sens ci-dessus, car la fonction réciproque 精 料 t = t ⁰ + 精^1/p n’est pas dérivable pour 精 = 0. On a alors:

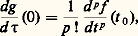et, par suite, l’arc paramétré défini par l’application g est régulier pour 精 = 0 et il a la même trajectoire que l’arc défini par f . On peut dire qu’on a une singularité «cinématique», due au paramétrage, et non une singularité de la trajectoire. Par exemple, l’arc paramétré défini par x = t ³, y = t ⁶, z = t ⁹ a une singularité pour t = 0, mais, si on pose 精 = t ³, on obtient x = 精, y = 精², z = 精³, qui est un arc paramétré sans singularité.

Si p est pair , on ne peut pas éliminer la singularité par changement de paramètre. On dit que la trajectoire présente un point de rebroussement . Au voisinage d’un tel point, la courbe présente l’aspect indiqué par la figure 4; si q est impair, on dit qu’on a un point de rebroussement de première espèce (cf. la cycloïde, fig. 2); si q est pair, on dit qu’on a un point de rebroussement de deuxième espèce.

Élément de longueur

Jusqu’à présent, nous n’avons pas utilisé la structure euclidienne de l’espace; nous allons en faire usage pour choisir un paramètre admissible privilégié au voisinage d’un point régulier. On appelle abscisse curviligne un paramètre s tel que, pour g (s ) = f (t ), le vecteur vitesse dg /ds soit unitaire. Comme:

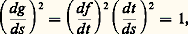on doit avoir:

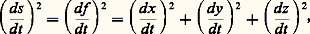d’où:

choisir le signe de s 漣 s ⁰, c’est orienter la trajectoire en choisissant un «sens de parcours».

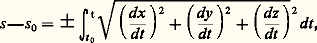Si f définit un arc paramétré, l’intégrale:

s’appelle la longueur de l’arc A = f ([a , b ]). Cette longueur est invariante par changement de paramètre admissible et peut s’interpréter ainsi: à chaque subdivision finie t ⁰ = a 麗 t ¹ 麗 t ² 麗 ... 麗 t ^n-1 麗 t ⁿ = b de l’intervalle [a , b ], associons la longueur de la ligne polygonale joignant les points f (t ⁱ ):

alors la longueur L est la borne supérieure de ces nombres pour toutes les subdivisions finies de [a , b ].

Par exemple, la longueur du cercle de rayon R est: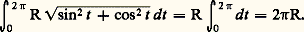

Pour la cycloïde, la longueur d’un arc compris entre deux points de rebroussement successifs est:

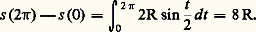Trièdre de Frénet

Nous allons continuer l’étude locale d’un arc paramétré au voisinage d’un point régulier en associant à chaque point de la trajectoire un trièdre orthonormé de sens direct.

Si on prend pour paramètre au voisinage d’un point régulier l’abscisse curviligne s , alors, par définition, le vecteur vitesse:

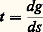est unitaire. Si le vecteur d t/ds n’est pas nul, il est orthogonal au vecteur t; on posera:

où n est un vecteur unitaire et R un nombre positif appelé rayon de courbure si la courbe est non plane (dans le cas d’une courbe plane, on choisit le vecteur n directement perpendiculaire et R est un nombre réel de signe quelconque); on appelle alors centre de courbure le point P défini par P = M + Rn. Remarquons que si on change l’orientation de la trajectoire, s 料 漣 s et t 料 漣 t, le vecteur d t/ds ne change pas d’orientation. Définissons alors le vecteur b par la formule: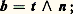

le trièdre t, n, b s’appelle le trièdre de Frénet. On a les formules:

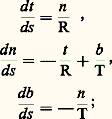les fonctions 1/R(s ) et 1/T(s ) s’appellent respectivement la courbure et la torsion de la trajectoire. Au voisinage d’un point régulier, les projections de la trajectoire sur les trois plans définis par t, n, b présentent l’aspect indiqué par la figure 5.

On démontre que si deux trajectoires ont même courbure et même torsion pour tout s , alors il existe un déplacement euclidien transformant l’une en l’autre. Si 1/T = 0 pour tout s , la trajectoire est plane; si 1/R = 0, alors la torsion est nulle et la trajectoire est une droite.

4. Courbes régulières

Nous sommes enfin capables de donner une définition correcte de la notion de courbe régulière.

Par définition, une courbe régulière C, de classe C^k , de l’espace euclidien E³ ou E² est un sous-ensemble qui possède la propriété suivante: Tout point x 捻 C est centre d’une boule ouverte B (resp. d’un disque ouvert B) telle qu’il existe un arc paramétré f : IE³ (ou E²), de classe C^k , tel que f (t ) 0 pour tout t 捻 I, qui soit un homéomorphisme de I sur C 惡 B. Ainsi C est une réunion de trajectoires d’arc paramétrés sans points singuliers. Si (f ⁱ , Iⁱ ) et (f ^j , I^j ) sont deux représentations paramétriques telles que I^ij = f ⁱ (Iⁱ ) 惡 f ^j (I^j ) ne soit pas vide, alors, f ^{j -1} 獵f ⁱ , défini dans f ^{i -1}(I^ij ), est un changement de paramètre admissible. Ce qui précède sur les arcs paramétrés montre qu’on peut définir la tangente en chaque point ainsi que, quand le plan osculateur est défini, le trièdre de Frénet. Remarquons qu’une courbe aussi simple que la cycloïde ne rentre cependant pas dans ce cadre, car elle présente des points singuliers.

Le théorème des fonctions implicites entraîne que si F est une fonction numérique sur E², différentiable de dérivée ne s’annulant pas sur ^-1(a ) pour un nombre réel a , l’ensemble ^-1(a ) est une courbe régulière; de même, dans E³, si deux fonctions ¹ et ² sont indépendantes, l’ensemble défini par ¹ = constante et ² = constante est une courbe régulière. Par exemple, dans le plan, l’équation:

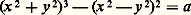représente une courbe régulière pour a 0, car la différentielle de F(x , y ) = (x ² + y ²)³ 漣 (x ² 漣 y ²)² ne s’annule que pour x = y = 0, et alors F(0, 0) = 0. Par contre, l’équation (x ² + y ²)³ 漣 (x ² 漣 y ²)² = 0 représente une courbe présentant une singularité à l’origine: c’est le «trèfle à quatre feuilles» vu ci-dessus (fig. 1).

Enfin, une courbe régulière est dite orientée si tous les changements de représentation paramétrique f ^{j -1} 獵 f ⁱ sont des fonctions croissantes.

On peut démontrer pour les courbes fermées régulières planes les deux théorèmes suivants: l’angle dont «tourne» le vecteur unitaire tangent à une telle courbe orientée est 梁 2 神; pour toute courbe fermée convexe (c’est-à-dire ne présentant pas d’inflexion, et par suite pour laquelle la courbure garde un signe constant) il y a au moins quatre sommets (c’est-à-dire des points où la courbure présente un extrémum).

5. Définition des surfaces

Surfaces régulières

On appellera surface régulière de classe C^k , k 閭 1, de l’espace euclidien E³ un sous-ensemble S 說 E³ possédant la propriété suivante: Tout point de S est centre d’une boule ouverte B de E³ telle qu’il existe une application 﨏 de classe C^k d’un ouvert U de R² dans E³:

de rang 2 en tout point de U, qui soit un homéomorphisme de U sur S 惡 B. Si 﨏 = ( 﨏¹, 﨏², 﨏³), où 﨏¹, 﨏² et 﨏³ sont des fonctions numériques de classe C^k , la condition sur le rang signifie que la matrice:

est de rang 2, ou encore que le produit vectoriel:

est un vecteur non nul.

L’application 﨏 est appelée une représentation paramétrique vraie , ou régulière , de V = S 惡 B. Il résulte alors du théorème des fonctions implicites qu’au voisinage de chaque point de S on peut exprimer l’une des coordonnées comme fonction de classe C^k des deux autres, l’application ainsi définie étant de rang 2. Si ( 﨏ⁱ , Uⁱ ) et ( 﨏^j , U^j ) sont deux représentations paramétriques telles que V^ij = 﨏ⁱ (Uⁱ ) 惡 﨏^j (U^j ) ne soit pas vide, le changement de paramètre 﨏^{j -1} 獵 﨏ⁱ est un difféomorphisme de classe C^k de 﨏^{i -1}(V^ij ) sur 﨏^{j -1}(V^ij ) (fig. 6). Ces considérations conduisent directement à la notion de variété différentiable générale ^{[cf. VARIÉTÉS DIFFÉRENTIABLES]}.

Par exemple, pour la sphère S de centre O et de rayon 1, la représentation paramétrique: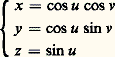

n’est pas régulière aux pôles. Par contre, au moyen d’une projection stéréographique de pôle (P(0, 0, 1), on définit une application de classe C^k de R² sur S 漣P:

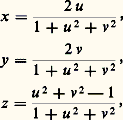qui est un homéomorphisme. De même, l’inversion de pôle P (0, 0, 漣 1) applique R² sur S 漣P:

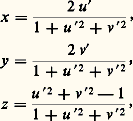dans R² 漣O, le changement de paramètre est l’inversion de pôle O et de puissance 1:

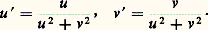En utilisant le fait que S est compacte (fermée et bornée dans R³), on peut montrer qu’il n’existe aucune représentation paramétrique régulière de la sphère tout entière.

De manière générale, soit f une fonction numérique de classe C^k définie dans E³ ; si a 捻 f (E³) est tel que f soit de rang 1 (c’est-à-dire que sa différentielle ne s’annule pas) en tout point de f ^-1(a ), alors le théorème des fonctions implicites entraîne que l’ensemble f ^-1(a ) est une surface régulière. Par exemple, la sphère est définie par l’équation:

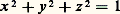S’il existe des points de f ^-1(a ) où la différentielle s’annule, on dit que f ^-1(a ) est une surface avec singularités ; par exemple le cône x ² + y ² 漣 z ² = 0, vu au chapitre 2, a l’origine pour point singulier (sommet du cône).

Comme exemples importants de surfaces régulières, on a notamment les quadriques (à l’exclusion du cône) définies par une équation:

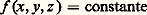où f est un polynôme de degré 2 ^{[cf. QUADRIQUES]}, par exemple l’hyperboloïde à une nappe :

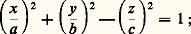il admet la représentation paramétrique:

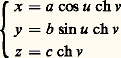qui n’est pas régulière, car non bijective. Par contre, cette représentation paramétrique définit un difféomorphisme de S¹ 憐 R sur la surface, en désignant par S¹ le cercle de centre O et de rayon 1. Un autre exemple est le paraboloïde hyperbolique («selle de cheval») d’équation:

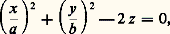qui est difféomorphe à R² (fig. 10).

On dit qu’une surface S est réglée si par tout point de S passe au moins une droite entièrement contenue dans S; une telle droite est appelée une génératrice de la surface (fig. 7 et 8). Par exemple, l’hyperboloïde à une nappe et le paraboloïde hyperbolique sont engendrés par deux familles à un paramètre de droites: par chaque point passe une génératrice de chaque famille.

Parmi les autres surfaces d’un type particulier, notons les surfaces de révolution : une surface S (régulière ou avec singularités) est dite de révolution autour d’un axe D si toute rotation d’axe D transforme S en elle-même. Ainsi, si M est un point de S qui n’appartient pas à D, le cercle d’axe D passant par M est entièrement situé dans S; on dit qu’un tel cercle est un parallèle de la surface. De même, on appelle méridien les intersections de S avec les plans passant par D; bien entendu, la terminologie précédente généralise celle adoptée traditionnellement pour la sphère qui est de révolution autour de tout axe passant par son centre. Par exemple, pour a = b , l’hyperboloïde à une nappe est de révolution autour de l’axe Oz ; c’est la surface engendrée par la rotation d’une droite autour d’un axe non coplanaire et les méridiens sont des hyperboles. Le tore est défini par la rotation d’un cercle autour d’une droite de son plan ne le rencontrant pas (fig. 11). Il admet la représentation paramétrique (non régulière, parce que non bijective):

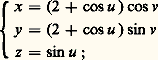cette représentation paramétrique définit un difféomorphisme de S¹ 憐 S¹ sur le tore, en désignant toujours par S¹ le cercle de rayon 1.

Plan tangent

Soit M un point d’une surface régulière (ou un point régulier d’une surface avec singularités). Si ( 﨏, U) est une représentation paramétrique régulière au voisinage de M, l’image de R² par l’application affine ^M 﨏 tangente à 﨏 au point m = 﨏^-1(M) (cf. chap. 1) est indépendante du choix de la représentation paramétrique régulière: cette image est le plan, passant par M, engendré par les vecteurs:

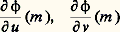appelé plan tangent à la surface en M. On le désignera par ^MS. Ce plan tangent est l’ensemble engendré par les tangentes en M aux courbes régulières passant par ce point et tracées sur S. De manière précise, cela signifie que, pour tout arc paramétré régulier 塚 tel que 塚(t ⁰) = M dont la trajectoire est contenue dans S, le vecteur vitesse (d 塚/dt )(t ⁰) d’origine M appartient au plan tangent; de plus, si 﨏: US, U 說 R² est une représentation paramétrique de S, l’application 塚 se factorise localement sous la forme 塚 = 﨏 獵 f , où f est un arc paramétré de U, c’est-à-dire que l’arc paramétré est défini par u = f ¹(t ), v = f ²(t ) si f = (f ¹, f ²). En particulier les vecteurs (face=F0019 煉 﨏/ 煉u )(m ) et (face=F0019 煉 﨏/ 煉v )(m ) correspondent respectivement à v = constante et u = constante. Réciproquement , pour tout vecteur V 捻 ^MS, il existe une application f : IU telle que le vecteur vitesse:

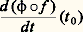soit égal au vecteur V.

Si la surface est réglée, toute génératrice passant par M appartient au plan tangent; en particulier, s’il passe par M deux génératrices distinctes, elles engendrent le plan tangent: c’est ce qui se produit pour l’hyperboloïde à une nappe et pour le paraboloïde hyperbolique (fig. 10). Dans le cas particulier où le plan tangent est le même tout le long de chaque génératrice, on dit qu’on a une surface réglée développable.

Examinons les différentes surfaces réglées développables. Si toutes les génératrices passent par un point fixe, on a un cône ; si elles sont parallèles à une direction fixe, on a un cylindre . Un autre exemple très important s’obtient à partir des tangentes à une courbe: l’ensemble des tangentes à une courbe régulière engendre une surface développable. On peut montrer que la surface développable la plus générale est formée de nappes de surfaces coniques, cylindriques et de tangentes à des courbes gauches, ces nappes étant attachées les unes aux autres le long d’une génératrice (deux nappes se «recollant» le long d’une génératrice ont même plan tangent).

Position par rapport au plan tangent

Au voisinage d’un point M⁰(x ⁰, y ⁰, z ⁰) régulier d’une surface S, on peut exprimer une des coordonnées en fonction des deux autres, par exemple z = g (x , y ). Le plan tangent en M⁰ est alors défini par:

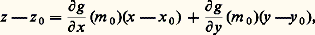où m ⁰ est le point (x ⁰, y ⁰); par un changement de repère euclidien, on peut ramener M⁰ à l’origine des coordonnées, soit x ⁰ = y ⁰ = z ⁰ = 0, le plan tangent en ce point à S étant défini par z = 0, soit (face=F0019 煉g / 煉x )(m ⁰) = 0 et (face=F0019 煉g / 煉y )(m ⁰) = 0. Le nombre z = g (x , y ) représente alors la distance «algébrique» du point M (x , y , g (x , y )) de la surface au plan tangent en M⁰. La formule de Taylor donne:

où on a adopté les notations de Monge: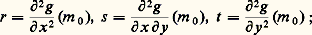

le reste R² est ici une quantité qui tend vers 0 plus vite que x ² + y ² quand (x , y ) tend vers (0, 0).

Si la forme quadratique associée à la différentielle seconde de g :

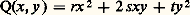est nulle (r = s = t = 0), on dit que le point M⁰ est plat ; la surface et son plan tangent ont alors un contact d’ordre supérieur à 1. Par exemple, la surface d’équation z = x ³ 漣 3 xy ² («selle de singe») a un point plat à l’origine; elle coupe son plan tangent à l’origine suivant trois droites et traverse ce plan tangent (fig. 9). Par contre, la surface z = x ²y ², qui présente elle aussi un point plat à l’origine, coupe le plan tangent en ce point suivant deux droites et reste d’un même côté de ce plan tangent (fig. 9).

Si la forme quadratique Q est non nulle, on distingue trois cas (fig. 10):

a ) Si rt 漣 s ² 礪 0, la forme Q est définie positive ou négative. Au voisinage de M⁰, l’intersection de S et du plan tangent en M⁰ se réduit à M⁰ et la surface reste d’un même côté de ce plan tangent (elle est localement convexe). C’est le cas de tous les points d’un ellipsoïde. On dit que le point M⁰ est elliptique.

b ) Si rt 漣 s ² 麗 0, la surface traverse son plan tangent au voisinage de M⁰. C’est le cas de tout point d’un hyperboloïde à une nappe ou d’un paraboloïde hyperbolique. On dit que le point est hyperbolique.

c ) Si rt 漣 s ² = 0, on ne peut rien dire de général. Même si la surface reste localement d’un même côté du plan tangent (point parabolique ), l’intersection ne se réduit pas nécessairement à un point. C’est le cas de tout point d’un cylindre elliptique ou parabolique; l’intersection avec un plan tangent est ici une génératrice.

Une même surface peut présenter des points de nature différente. Par exemple, le tore, dont on a donné une représentation paramétrique ci-dessus, admet des points elliptiques (tels que x ² + y ² 礪 1), des points hyperboliques (tels que x ² + y ² 麗 1; fig. 11) et des points paraboliques (tels que x ² + y ² = 1). L’ensemble des points paraboliques est constitué de deux parallèles au tore, le plus «haut» et le plus «bas», et en un tel point de plan tangent touche le tore tout le long du parallèle correspondant.

6. Formes fondamentales sur une surface

On appelle première forme fondamentale sur une surface S la forme quadratique 淋 qui, à tout vecteur V tangent à S en M, associe le carré de sa longueur, soit:

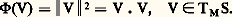Si au voisinage de M la surface S admet pour représentation paramétrique (u , v ) 料 﨏 (u , v ), on écrit:

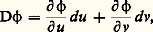et on a:

en posant: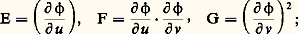

justifions ces notations. Si 塚 est un arc paramétré, dont le vecteur vitesse en M est égal à V, qui se factorise sous la forme 塚 = 﨏 獵 f (avec les notations du chapitre précédent), alors on a:

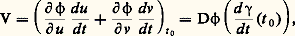et par suite:

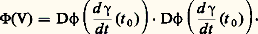Définissons maintenant la deuxième forme fondamentale; il sera pour cela nécessaire d’orienter la surface. Si la représentation paramétrique 﨏: US, U 說 R² est régulière en tout point M de 﨏(U), le produit vectoriel:

où m = 﨏^-1(M) 捻 U, est non nul; on peut donc associer à chaque point M de 﨏(U) un vecteur unitaire n normal à S de même sens que le produit vectoriel précédent, c’est-à-dire on oriente la surface. Si un arc paramétré:

se factorise sous la forme 塚 = 﨏 獵 f (cf. infra ), alors le produit scalaire:

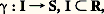
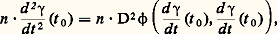où D² 﨏 est la dérivée seconde de 﨏, ne dépend que du vecteur tangent:

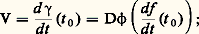en effet, on a:

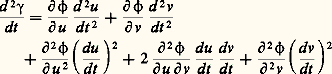d’où: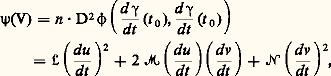

en posant:

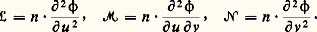La forme quadratique 祥: V 料 祥(V) est appelée la deuxième forme fondamentale de la surface. On démontre que la quantité:

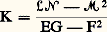est indépendante de la représentation paramétrique. En particulier, pour la représentation paramétrique z = g (x , y ) utilisée dans le chapitre précédent (avec p = q = 0 en M), on a:

ce scalaire K s’appelle la courbure totale , ou courbure de Gauss, en M. Suivant le signe de K, le point est elliptique, hyperbolique ou parabolique (cf. chap. 5, Position par rapport au plan tangent); remarquons que, puisque la forme quadratique 淋 est définie positive, le signe de K est celui de 硫類 漣 紐².

C. Gauss a démontré que la courbure totale était déterminée par E, F, G et leurs dérivées partielles premières. Étant donné deux surfaces S et S , on appelle isométrie locale de S dans S un difféomorphisme d’un ouvert U de E³ dans E³, appliquant S 惡 U dans S et transformant en chaque point M de S 惡 U la première forme fondamentale de S en la première forme fondamentale de S ; par suite, une isométrie locale laisse invariante la courbure totale. En particulier, une surface S telle qu’il existe en chaque point M 捻 S une isométrie d’un voisinage de ce point dans S sur un ouvert plan est dite applicable sur le plan ; puisque, pour un plan, la deuxième forme fondamentale est nulle, la courbure totale d’une surface applicable sur un plan est nulle. On démontre que toute surface à courbure totale nulle est une surface développable et que toute surface développable est applicable sur le plan.

Plus généralement, on montre que si deux surfaces S et S ont une courbure totale constante (cette constante étant la même pour les deux surfaces), il existe des isométries locales de S sur S’. Si la courbure totale est une constante positive, on dit que la surface est une surface sphérique; parmi ces surfaces figurent la sphère, et les surfaces sphériques de révolution du type hyperbolique et du type elliptique (fig. 12). Si la courbure totale est constante négative, on a les surfaces pseudosphériques; celles qui sont de révolution se répartissent en trois types indiqués par la figure 13.

Enfin, signalons qu’on démontre qu’une isométrie locale qui conserve aussi la deuxième forme fondamentale est la restriction d’un déplacement euclidien; par suite, l’ensemble des deux formes fondamentales caractérise localement une surface.

7. Courbes tracées sur une surface

Soit C une courbe régulière orientée tracée sur une surface régulière S; à tout point M de C on va attacher un repère, appelé trièdre de Darboux , obtenu de la manière suivante: soit t, n, b le trièdre de Frénet de la courbe C au point M; le trièdre de Darboux e ¹, e ², e ³ s’obtient en prenant pour e ³ le vecteur unitaire normal en M à la surface associé à l’orientation de cette surface, et en prenant e ¹ = t (et e ² = e ³ 廬 e ¹ pour obtenir un trièdre direct). Si s est l’abscisse curviligne sur C, on a alors les formules:

les nombres 1/ 福^g , 1/ 福ⁿ et 1/ 精^g ainsi définis s’appellent respectivement la courbure géodésique , la courbure normale et la torsion géodésique en M. Si 福 et 精 sont la courbure et la torsion de C en M, on a, en désignant par l’angle des deux vecteurs n et e ³: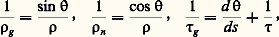

La courbure normale 1/ 福ⁿ en M est la même pour toutes les courbes tracées sur S qui admettent la même tangente en ce point M; en effet, 1/ 福ⁿ = e ³. (d ²M/ds ²), ce qui entraîne que cette courbure normale est égale à 祥(e ¹), en désignant par 祥 la deuxième forme fondamentale. On en déduit le théorème de Meusnier : Si un plan P pivote autour d’une droite du plan tangent ^MS, alors le centre de courbure (en M) de la section de S par P décrit un cercle passant par le point M. Un point d’une surface S pour lequel la courbure normale est la même dans toutes les directions est appelé un ombilic.

Une courbe tracée sur S est appelée une ligne asymptotique si la courbure normale en chacun de ses points est nulle; en chaque point, tout vecteur tangent à une telle courbe annule la deuxième forme fondamentale. Par suite, il ne passe de lignes asymptotiques que par les points hyperboliques (deux directions asymptotiques) ou paraboliques (une direction asymptotique). Toute droite tracée sur une surface est une ligne asymptotique.

On appelle lignes de courbure les lignes dont la torsion géodésique en chaque point est nulle, et on montre que cette condition équivaut à dire que les normales à la surface S le long d’une telle courbe engendrent une surface développable; ces normales sont les tangentes à la courbe décrite par les centres de courbure de la ligne de courbure. En chaque point régulier qui n’est pas un ombilic, il existe deux directions du plan tangent, appelées directions principales , perpendiculaires entre elles, pour lesquelles la courbure normale atteint son maximum 1/R¹ et son minimum 1/R²; les lignes de courbure peuvent aussi être définies comme les courbes tangentes en chaque point aux directions principales (fig. 14). La courbure totale est reliée simplement aux courbures des lignes de courbure par la formule:

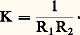Sur une surface dont tous les points sont des ombilics, toutes les courbes sont lignes de courbure; les seules surfaces possédant cette propriété sont les plans (K = 0) et les sphères (K = 1/R² constant).

On appelle géodésiques les courbes dont la courbure géodésique est nulle, c’est-à-dire dont la normale principale est normale à la surface; les géodésiques sont définies par un système d’équations différentielles du second ordre, et on démontre que par tout point d’une surface il passe une géodésique et une seule admettant une tangente donnée. De même, par deux points M et M de S assez voisins passe une géodésique et une seule: la longueur de l’arc de géodésique MM réalise alors le minimum de la longueur des arcs joignant M à M (cf. calcul des VARIATIONS). Par exemple, les géodésiques du plan sont les droites; les géodésiques d’une sphère sont les grands cercles, sections de la sphère par les plans passant par le centre, et par deux points non diamétralement opposés passe un tel grand cercle et un seul. Les géodésiques d’un cylindre de révolution sont les parallèles et les hélices circulaires.

On montre que la courbure géodésique ne dépend que de la première forme fondamentale; par suite, une isométrie locale applique les géodésiques sur les géodésiques.

8. Propriétés globales liées à la courbure totale

Soit 塚: IS un arc paramétré d’une surface S. Si X = X(t ) est un champ de vecteurs le long de la courbe C = 塚(I), on définit la dérivée covariante DX/dt du champ X au point M = 塚(t ) en projetant le vecteur d X/dt sur le plan tangent ^MS parallèlement à la normale. On dit alors que le champ X se déplace par parallélisme , ou est parallèle, si pour tout t 捻 I la dérivée covariante est nulle. Remarquons que la valeur X(t ⁰) du champ en un point détermine alors le champ parallèle. En particulier, on dit qu’un arc paramétré est géodésique si sa vitesse se déplace par parallélisme; une courbe géodésique devient un arc géodésique si on prend pour paramètre l’abscisse curviligne s ou tout autre paramètre t = as + b , a et b constants avec a 0.

Si la courbure totale n’est pas nulle, le transport par parallélisme le long d’un lacet (c’est-à-dire un arc paramétré 塚: [a , b ]S tel que 塚(a ) = 塚(b ) ne ramène pas en général le vecteur X(a ) à sa position initiale et, par suite, si on considère deux points M et M , le transport par parallélisme de M à M dépend du chemin choisi. En effet, on démontre que la «variation de l’angle» du vecteur X par transport parallèle le long d’un lacet est l’intégrale:

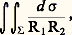où est la partie de S limitée par le lacet et d 靖 l’élément d’aire sur S.

D’autre part, on montre que si le lacet 塚 se compose d’un nombre fini d’arcs différentiables 塚^k séparés par des points anguleux où l’angle du vecteur tangent à 塚 subit une discontinuité ⁱ , on a:

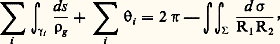formule de Gauss-Bonnet. Dans le cas particulier où 塚 est un triangle géodésique , c’est-à-dire un triangle curviligne dont les côtés sont des arcs géodésiques, l’intégrale de la torsion géodésique est nulle. Si on désigne par 見¹, 見², 見³ les mesures en radian (comprises entre 0 et 2 神) des angles du triangle, on a, puisque ces angles sont les supplémentaires de ceux qui interviennent dans la formule de Gauss-Bonnet:

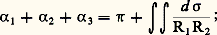pour le plan on retrouve le résultat classique que la somme des angles d’un triangle est égale à 神. Sur une sphère de rayon R, on a:

où A est l’aire du triangle. Remarquons que si la courbure totale est négative en tout point de S, alors la somme des angles d’un triangle géodésique est inférieure à 神. On retrouve que les surfaces à courbure constante constituent des modèles pour les géométries non euclidiennes de Riemann et de Lobatchewski.

Si on considère maintenant une surface compacte (c’est-à-dire fermée et bornée) sans bord, on montre qu’on peut la trianguler, c’est-à-dire la découper en domaines limités par des triangles curvilignes (pas nécessairement géodésiques). Appliquant la formule de Gauss-Bonnet à chaque triangle et faisant la somme, on obtient, puisque chaque arc est parcouru deux fois en sens contraires: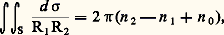

où n ², n ¹ et n ⁰ sont respectivement le nombre de triangles, le nombre d’arêtes et le nombre de sommets de la triangulation. Le premier membre étant indépendant de la triangulation, il en est de même du second. Le nombre entier positif:

est appelé la caractéristique d’Euler-Poincaré de la surface; par exemple, pour la sphère il est égal à 2, car: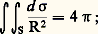

pour le tore, la caractéristique d’Euler-Poincaré est nulle.

On montre que la caractéristique d’Euler-Poincaré est un invariant topologique de la surface. On montre aussi qu’il existe, sur une surface S, un champ différentiable de vecteurs tangents ne s’annulant en aucun point si, et seulement si, la caractéristique d’Euler-Poincaré est nulle; il n’existe donc pas de tel champ sur une sphère.

Encyclopédie Universelle. 2012.